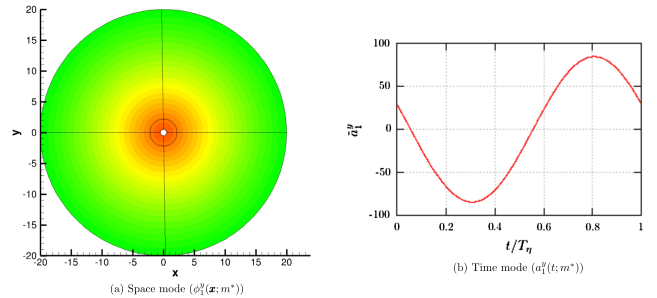
Galerkin projection of Navier–Stokes equations on proper orthogonal decomposition (POD) basis is predominantly used for model reduction in fluid dynamics. Robustness for changing operating conditions, numerical stability in long-term transient behavior and the pressure-term consideration are generally the main concerns of the Galerkin-POD reduced-order models (ROM). We develop a novel procedure to construct an off-reference solution state by using an interpolated POD reduced basis. A linear interpolation of the POD reduced basis is performed by using two reference solution states (see Fig.1). The POD basis functions are optimal in capturing the averaged flow energy. The energy dominant POD modes and corresponding base flow are interpolated according to the change in operating parameter (see Fig.2). The solution state is readily built without performing the Galerkin projection of the Navier–Stokes equations on the reduced POD space modes as well as the following time-integration of the resulted ordinary differential equations (ODE) to obtain the POD time coefficients. The proposed interpolation based approach is thus immune from the numerical issues associated with Galerkin-POD ROM.
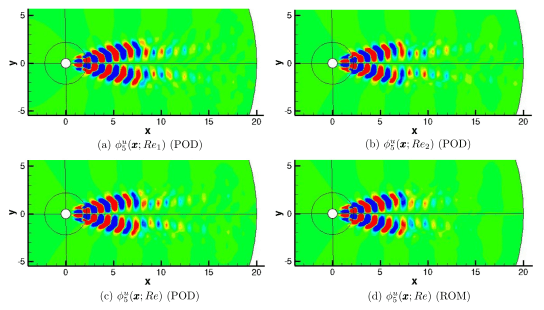
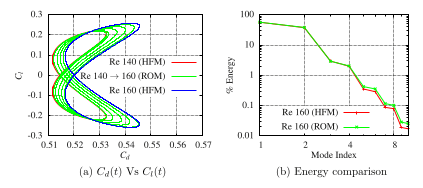
One of the main features of the Galerkin-free formulation of ROM is that it can be conveniently extended to multiphysics systems. We demonstrate its extension for fluid-structure interaction systems, where we consider both the incompressible and compressible flow regimes. The two case studies include: vortex induced vibration in a cylinder at Re=100 and shock wave transitional boundary layer induced panel flutter at Mach 2. The reduced basis is comprised of the dominant POD modes for the mesh deformation (Fig.1).
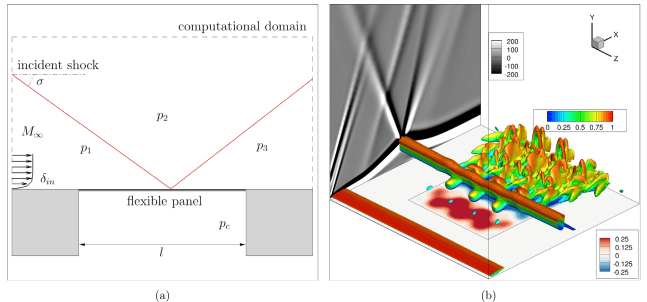
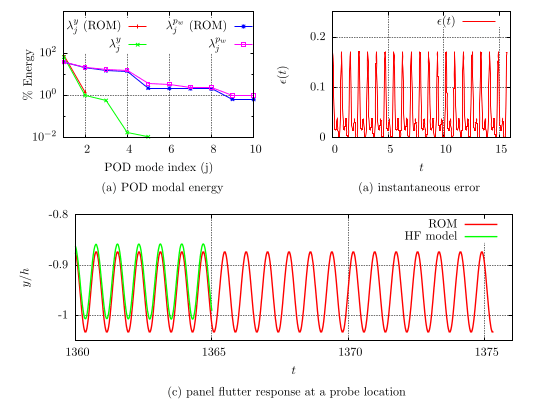
We conveniently extend the Galerkin-free ROM formulation for a high-speed compressible flow, where the flow configuration is comprised of shock wave transitional boundary layer interaction over a flexible panel (Fig.4). In this case study, we construct ROM by considering only the bottom surface of the computational domain and using the wall pressure and panel deflection as the solution state variables. The ROM predictions for an off-reference case, for different panel thickness, are in good agreement with the high-fidelity simulation results (Fig. 5).
In general, reduced-order models face difficulty for transitional flow physics. An increase of number of reference states and higher order interpolations across the transitional regime are a couple of remedies.