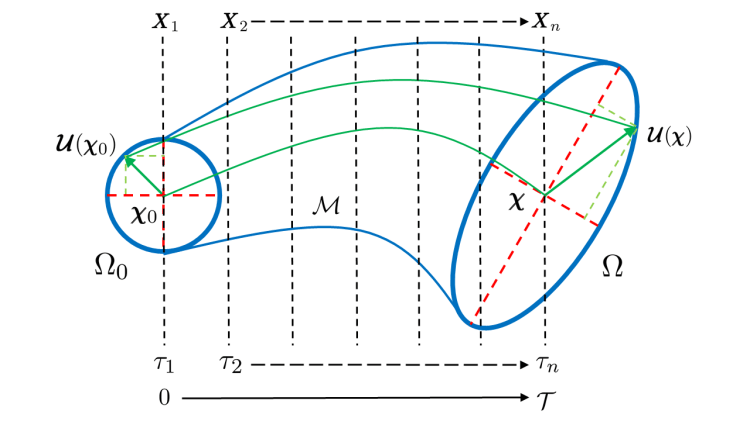
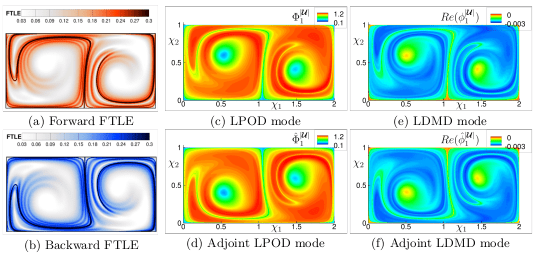
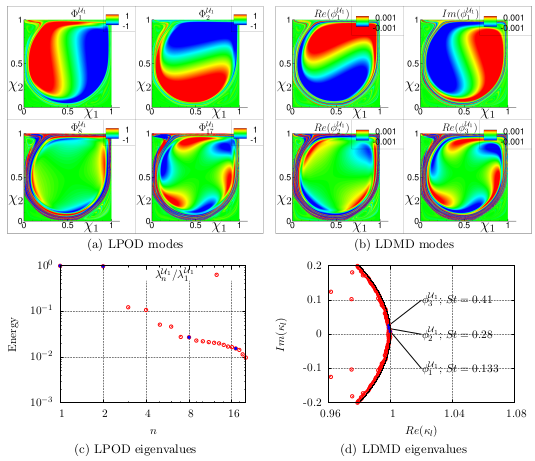
Modal decomposition finds common use in flowfield analysis, data-driven modeling and flow control. Among the more popular techniques are proper orthogonal decomposition (POD) and dynamic mode decomposition (DMD). Modal analysis is most often performed in an Eulerian (fixed) frame of reference using unsteady flow snapshots obtained from experimental measurements or solutions to the governing equations. The Eulerian description poses some difficulties, however, when the domain or the mesh deforms with time, such as for example in fluid-structure interactions, where the walls respond to fluid forces and body-fitted meshes must necessarily also vary in time. In such cases, modal decomposition may be more elegantly performed in a suitably constructed Lagrangian frame. In this work, we first formulate a Lagrangian modal analysis (LMA) ansatz by a posteriori transforming the Eulerian flow fields into Lagrangian flow maps through an orientation and measure-preserving domain diffeomorphism. The development of LMA for POD and DMD is then verified using direct numerical simulations (DNS) of two canonical flow configurations, the lid-drive cavity and flow past a cylinder, to represent internal and external flows, respectively. Various Reynolds numbers are considered for each problem to represent pre- and post-bifurcation dynamics at Mach 0.5. The LMA is demonstrated for several situations encompassing unsteady flow without and with mesh deformation as well as non-uniform base flows that are steady in the Eulerian but not in the Lagrangian frame. In particular, the LMA on steady non-uniform base flow gives insights into the flow stability and post-bifurcation dynamics. The development of LMA naturally leads to Lagrangian coherent flow structures and connections with Lyapunov exponents, important for chaos, stability and mixing studies. Thus, we devise the mathematical link between finite-time Lyapunov exponents (FTLE) and LMA, which is examined by considering a double-gyre flow pattern. The LMA is performed using forward and backward (adjoint) time procedures, to recover physically and dynamically important flow features, in the Lagrangian sense.