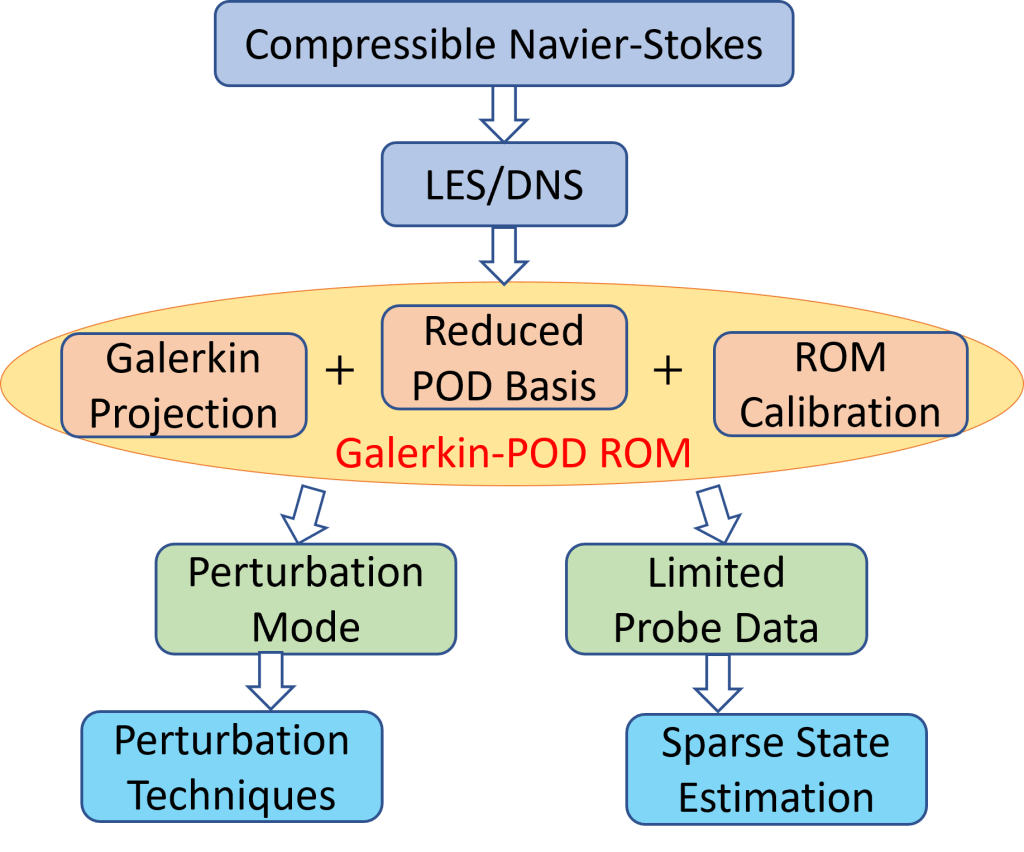
Perturbation techniques can provide valuable insights into flow control by identifying sensitive regions. However, performing such analyses with high-fidelity techniques, such as large eddy simulations or direct numerical simulations, can be computationally prohibitive. In this effort, we employ reduced-order modeling (ROM) of compressible Navier-Stokes equations based on the Galerkin-projection and proper orthogonal decomposition (POD) to explore the effect of flow perturbations on the flow. The effect of a perturbation mode with a given spatio-temporal form, in this case plasma-like actuation for concreteness, is introduced into the reduced POD basis. The flow field considered is a two-dimensional lid-driven cavity flow at Mach 0.5 at a post-bifurcation Reynolds number of Re_L = 15,000 based on the cavity length, L. The Galerkin-POD ROM ansatz is also used to present a full flow state estimator for highly sparse data by combining the reduced POD basis with limited/partial probe data. The Galerkin-POD ROM with the flow perturbation analyses and full state estimation yields a promising framework for flow control applications to a wide range of compressible flows.